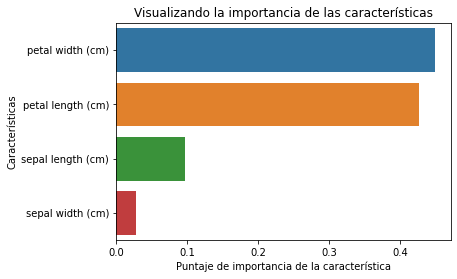Random Forest (Bosques Aleatorios)

Aprendizaje Supervisado / Clasificación⌗
Para poder comprender de qué trata el modelo de machine learning Random Forest es preciso antes hablar sobre los árboles de decisión. A contiuación se describe a grandes rasgos este concepto.
Arboles de decisión⌗
Introducción⌗
Los árboles de decisión son un popular método de aprendizaje supervisado siendo capaz de realizar tareas de regresión y clasificación. Los árboles de decisión son fáciles de utilizar y entender, y representan un buen método de exploración si el interés es tener una mejor idea acerca de las características más influyentes en el set de datos.
¿Cómo funciona?⌗
Los árboles de decisión aprenden una serie reglas if-else para los valores de las características/variables/atributos, este flujo de decisión (if-else) resulta en la predicción de una variable target.
Ejemplo⌗
Juego del si/no
{{ image src="/img/random-forest/decision_tree.png" alt=“Decision tree” position=“left” style=“border-radius: 8px;” }}
Este ejemplo consiste en un simple juego de preguntas cuyas respuestas deben ser si o no. Una persona x deberá adivinar un objeto (variable target) que la otra persona esté imaginando, realizando una serie de preguntas, cuyo objetivo es ir reduciendo las posibilidades hasta llegar a la respuesta correcta.
El flujo del ejemplo sería entonces:
-
¿Está vivo?
R. No -
¿Vuela?
R. No -
¿Puede llevar a más de 10 personas?
R. No -
Es un automóvil!
Si lo notas, este flujo entonces tomará la forma de un árbol invertido y de ahí sus conceptos relacionados como:
Arbol de decisión
- Nodo raíz: nodo base del árbol
- Nodo hoja: representan las clases del dataset y son la parte más externa del árbol (no tienen nodos "hijos").
Con esto, es posible entonces diseñar una serie de reglas que resulten en un algoritmo capaz de aprender y pueda categorizar un objecto/variable.
Ahora que tenemos una idea más clara sobre los árboles de decisión, podemos proceder a hablar sobre random forest.
Random Forest⌗
Introducción⌗
Random Forest es quizás uno de los métodos de Machine Learning más utilizados en el área de ciencia de datos y consiste en crear modelos de aprendizaje conocidos como ensamblajes (uniones). Un ensamble (ensemble) consiste en agrupar múltiples modelos de aprendizaje y combinarlos, lo que produce un modelo agregado que es mucho más "poderoso" (preciso) que los modelos individuales.
¿Por qué los ensamblajes son efectivos?⌗
Aunque tengamos diferentes modelos de aprendizaje que individualmente se desempeñen "bien" (tengan una precisión aceptable), de igual forma tenderán a cometer diferentes tipos errores en un set de datos. Esto ocurre típicamente porque cada modelo podría sobreajustarse a diferentes porciones del set de datos. Al combinar diferentes modelos individuales en un ensamblaje podemos promediar sus errores para así reducir el riesgo de sobreajuste y pueda generalizar con mayor eficacia.
Esta idea de ensamblaje es aplicada entonces al modelo Random Forest y dentro de éste podemos destacar:
-
Es un ensamblaje (agrupación) de muchos árboles de decisión.
-
Extensamente usado, debido a sus buenos resultados en diversos tipo de problemas.
-
módulo de scikit-learn -> sklearn.ensemble:
- Clasificación: RandomForestClassifier
- Regresión: RandomForestRegressor
-
Un solo árbol de decisión puede conlleva un riesgo de sobreajuste.
-
Muchos árboles de decisión: más estable, generaliza mejor.
-
El ensamblaje de árboles debiera ser diverso: introducir una variación al azar resulta provechoso en la construcción de árboles.
Proceso⌗
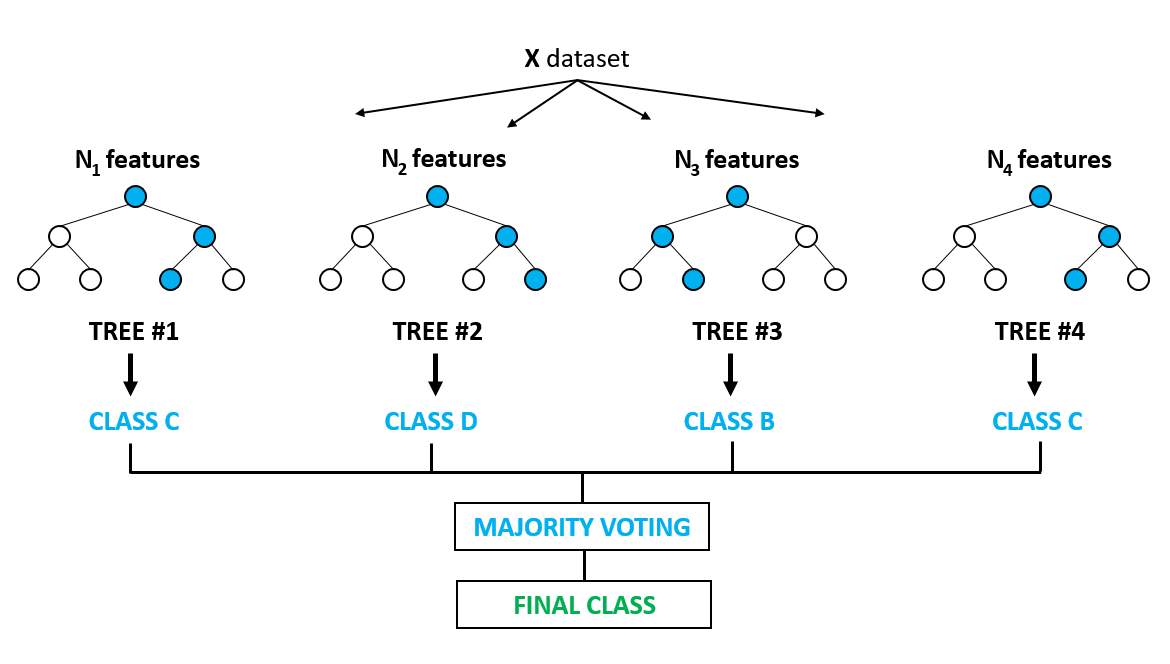
A nivel general los pasos que realiza el algoritmo son:
- Se divide el set de datos al azar para construir cada árbol de decisión (Bootstrap Samples / Instances)
- Se seleccionan las características al azar (max_features)
- Se define la cantidad de árboles a construir (n_estimator)
- Realiza una "votación" para cada resultado previsto.
- Selecciona el resultado de la predicción con más votos como la predicción final.
A tener presente
- El algoritmo es altamente sensitivo al parámetro max_features
- Cuando el parámetro max_features equivale a 1, el algoritmo creará bosques más diversos y complejos.
- Si el parámetro max_features se acerca al número de características, los bosques serán más similares y simples.
Desventajas
- Los bosques aleatorios son lentos en la generación de predicciones porque tiene múltiples árboles de decisión. Cada vez que hace una predicción, todos los árboles en el bosque tienen que hacer una predicción y luego votar sobre él. Todo este proceso lleva mucho tiempo.
- El modelo es difícil de interpretar en comparación con un árbol de decisión, donde puede tomar una decisión fácilmente siguiendo la ruta en el árbol.
Implementación⌗
- Importación de librerías y carga de dataset
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics
iris = datasets.load_iris()
print(iris.DESCR)
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
.. topic:: References
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
Planta Iris⌗
Especies⌗

- Imprime las etiquetas de las especies(setosa, versicolor,virginica)
print(iris.target_names)
['setosa' 'versicolor' 'virginica']
- Imprime las características del dataset
print(iris.feature_names)
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
- Imprime 5 1eros registros de los datos del dataset
print(iris.data[0:5])
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
- Imprime las etiquetas del dataset (0:setosa, 1:versicolor, 2:virginica)
print(iris.target)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
- Crea dataframe
data=pd.DataFrame({
'sepal length':iris.data[:,0],
'sepal width':iris.data[:,1],
'petal length':iris.data[:,2],
'petal width':iris.data[:,3],
'species':iris.target
})
data.head()
| sepal length | sepal width | petal length | petal width | species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 5.0 | 3.6 | 1.4 | 0.2 | 0 |
- Selección de características y etiquetas
X = data[['sepal length', 'sepal width', 'petal length', 'petal width']] # Características
y = data['species'] # Etiquetas
- Crea subconjuntos de datos (traning set y test set)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
- Crea modelo de tipo Random Forest (clasificador)
clf=RandomForestClassifier(n_estimators=100)
- Entrena el modelo con set de datos de entrenamiento
clf.fit(X_train,y_train)
- Crea predicciones con datos de testing
y_pred=clf.predict(X_test)
- Mide precisión del modelo
print("Precisión: ", metrics.accuracy_score(y_test, y_pred))
Precisión: 0.9333333333333333
df = pd.DataFrame({'Real': y_test, 'Predecido': clf.predict(X_test).flatten()})
df
| Real | Predecido | |
|---|---|---|
| 27 | 0 | 0 |
| 138 | 2 | 2 |
| 108 | 2 | 2 |
| 60 | 1 | 1 |
| 136 | 2 | 2 |
| 140 | 2 | 2 |
| 132 | 2 | 2 |
| 33 | 0 | 0 |
| 129 | 2 | 2 |
| 95 | 1 | 1 |
| 112 | 2 | 2 |
| 106 | 2 | 1 |
| 133 | 2 | 1 |
| 104 | 2 | 2 |
| 91 | 1 | 1 |
| 80 | 1 | 1 |
| 77 | 1 | 2 |
| 65 | 1 | 1 |
| 53 | 1 | 1 |
| 38 | 0 | 0 |
| 1 | 0 | 0 |
| 56 | 1 | 1 |
| 72 | 1 | 1 |
| 14 | 0 | 0 |
| 116 | 2 | 2 |
| 49 | 0 | 0 |
| 41 | 0 | 0 |
| 144 | 2 | 2 |
| 102 | 2 | 2 |
| 118 | 2 | 2 |
| 24 | 0 | 0 |
| 86 | 1 | 1 |
| 121 | 2 | 2 |
| 51 | 1 | 1 |
| 68 | 1 | 1 |
| 47 | 0 | 0 |
| 141 | 2 | 2 |
| 75 | 1 | 1 |
| 82 | 1 | 1 |
| 25 | 0 | 0 |
| 2 | 0 | 0 |
| 69 | 1 | 1 |
| 43 | 0 | 0 |
| 85 | 1 | 1 |
| 148 | 2 | 2 |
- Mide la “importancia/influencia” de cada una de las características
feature_imp = pd.Series(clf.feature_importances_, index=iris.feature_names).sort_values(ascending=False)
feature_imp
petal width (cm) 0.448239
petal length (cm) 0.426404
sepal length (cm) 0.096513
sepal width (cm) 0.028844
- Visualizamos los datos anteriores
%matplotlib inline
sns.barplot(x=feature_imp, y=feature_imp.index)
plt.xlabel('Puntaje de importancia de la característica')
plt.ylabel('Características')
plt.title("Visualizando la importancia de las características")
plt.show()