Support Vector Machine (SVM)
Máquinas de vectores de soporte⌗
Minería de datos
Introducción⌗
A continuación veremos cómo los modelos lineales pueden no sólo realizar tareas de regresión, sino también de clasificación. En esta labor utilizaremos la misma forma lineal de regresión, pero ahora en vez de predecir una variable continua (ej: sueldo, valor de una casa) buscaremos obtener un resultado binario para que nuestro algoritmo realice la clasificación.
A pesar de que en su origen se desarrolló como un método de clasificación binaria, su aplicación se ha extendido a problemas de clasificación múltiple y regresión. SVMs ha resultado ser uno de los mejores clasificadores para un amplio abanico de situaciones, por lo que se considera uno de los referentes dentro del ámbito de aprendizaje estadístico y machine learning.
¿Qué es?⌗
El algoritmo de Máquinas de vectores de soporte pertenece a la familia de algoritmos que utilizan aprendizaje supervisado para realizar sus predicciones. Es utilizado en tareas de clasificación como de regresión, pero en nuestro caso nos enfocaremos en cómo un modelo lineal es capaz de realizar una clasificación.
Este algoritmo se basa en los datos de entrenamiento etiquetados para generar un hiperplano que clasifica los nuevos ejemplos en dos espacios dimensionales. El hiperplano es la línea que divide al plano en dos partes, quedando cada clase a un lado.
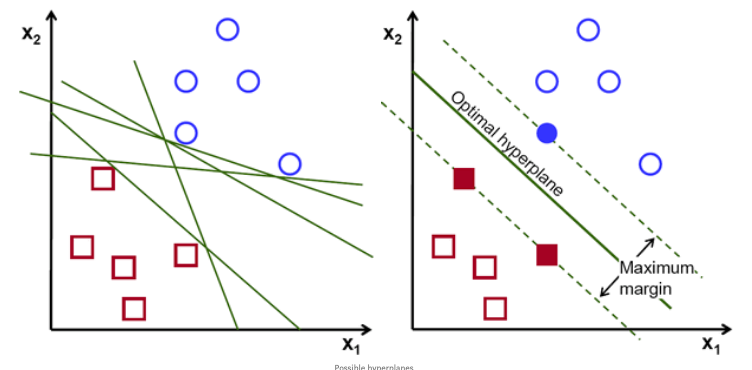
Como vemos en la imagen superior izquierda existen muchos hiperplanos posibles para dividir el plano y posteriormente el algoritmo haga la predicción (ej: 'cuadrado' , 'circulo'). Sin embargo, como nuestro trabajo científico requiere de precisión exacta y medible, el objetivo será encontrar el hiperplano (linea) óptimo para cada plano/dataset y así nuestro modelo obtenga resultados cuantificables (imagen derecha). Este hiperplano óptimo siempre buscará tener el máximo de margen posible, el cual se traduce en la distancia máxima entre los puntos de datos que representan a cada clase ('cuadrado', 'circulo'). Mientras más grande sea el margen, mayor precisión tendrá nuestro algoritmo en tareas de clasificación.
Aplicación⌗

A continuación, con la ayuda de scikit-learn implementaremos un algoritmo de tipo máquina de vectores de soporte cuyo objetivo será clasificar tipos de tumor mamario en benigno y maligno.
Cáncer de mama⌗
"El cáncer de mama es el cáncer más común entre las mujeres del mundo. Representa el 25% de todos los casos de cáncer y afectó a más de 2.1 millones de personas solo en 2015. Aparece cuando las células del seno comienzan a crecer sin control. Estas células generalmente forman tumores que pueden verse a través de rayos X o sentirse como bultos en el área del seno.
El diagnóstico temprano aumenta significativamente las posibilidades de supervivencia. Los desafíos clave contra su detección es cómo clasificar los tumores en malignos (cancerosos) o benignos (no cancerosos). Un tumor se considera maligno si las células pueden crecer en los tejidos circundantes o extenderse a áreas distantes del cuerpo. Un tumor benigno no invade el tejido cercano ni se propaga a otras partes del cuerpo como los tumores cancerosos, pero puede ser grave si presiona estructuras vitales como los vasos sanguíneos o los nervios.
La técnica de Machine Learning puede mejorar dramáticamente el nivel de diagnóstico en cáncer de seno. La investigación muestra que los médicos experimentados pueden detectar el cáncer con una precisión del 79%, mientras que se puede lograr una precisión del 91% (a veces hasta el 97%) utilizando técnicas de Machine Learning." (Adebola Lamidi)
Dataset⌗
El set de datos que trabajaremos en esta ocasión se calcula a partir de una imagen digitalizada de un aspirado con aguja fina (FNA) de una masa mamaria. Estos datos describen las características de los núcleos celulares presentes en la imagen.
El conjunto de datos contiene 30 características/atributos y como variable target (objetivo) a clasificar, el tipo de cáncer. Los tipos de cáncer se dividen en dos clases: maligno (dañino) y benigno (no dañino).
Importación y carga de datos⌗
# Importamos dataset de ejemplo incluido en librería scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.svm import SVC # importación de modelo
# cargamos dataset
cancer = datasets.load_breast_cancer()
Exploración y análisis de datos⌗
print(cancer.DESCR)
Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 569
:Number of Attributes: 30 numeric, predictive attributes and the class
:Attribute Information:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
The mean, standard error, and "worst" or largest (mean of the three
largest values) of these features were computed for each image,
resulting in 30 features. For instance, field 3 is Mean Radius, field
13 is Radius SE, field 23 is Worst Radius.
- class:
- WDBC-Malignant
- WDBC-Benign
:Summary Statistics:
===================================== ====== ======
Min Max
===================================== ====== ======
radius (mean): 6.981 28.11
texture (mean): 9.71 39.28
perimeter (mean): 43.79 188.5
area (mean): 143.5 2501.0
smoothness (mean): 0.053 0.163
compactness (mean): 0.019 0.345
concavity (mean): 0.0 0.427
concave points (mean): 0.0 0.201
symmetry (mean): 0.106 0.304
fractal dimension (mean): 0.05 0.097
radius (standard error): 0.112 2.873
texture (standard error): 0.36 4.885
perimeter (standard error): 0.757 21.98
area (standard error): 6.802 542.2
smoothness (standard error): 0.002 0.031
compactness (standard error): 0.002 0.135
concavity (standard error): 0.0 0.396
concave points (standard error): 0.0 0.053
symmetry (standard error): 0.008 0.079
fractal dimension (standard error): 0.001 0.03
radius (worst): 7.93 36.04
texture (worst): 12.02 49.54
perimeter (worst): 50.41 251.2
area (worst): 185.2 4254.0
smoothness (worst): 0.071 0.223
compactness (worst): 0.027 1.058
concavity (worst): 0.0 1.252
concave points (worst): 0.0 0.291
symmetry (worst): 0.156 0.664
fractal dimension (worst): 0.055 0.208
===================================== ====== ======
:Missing Attribute Values: None
:Class Distribution: 212 - Malignant, 357 - Benign
:Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian
:Donor: Nick Street
:Date: November, 1995
This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2
Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass. They describe
characteristics of the cell nuclei present in the image.
Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree. Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.
The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].
This database is also available through the UW CS ftp server:
ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/
.. topic:: References
- W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
San Jose, CA, 1993.
- O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
prognosis via linear programming. Operations Research, 43(4), pages 570-577,
July-August 1995.
- W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
163-171.
Obtenemos las características del dataset⌗
cancer.feature_names
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23')
Obtenemos variable target, la cual servirá para clasfificar el tipo de cancer(‘malignant’ ‘benign’)⌗
cancer.target_names
array(['malignant', 'benign'], dtype='<U9')
Creamos dataframe⌗
df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df.head()
Agregamos columna target no incluida⌗
df['target'] = cancer.target
df.head()
verificamos si dataset contiene valores nulos⌗
df.isnull().sum()
mean radius 0
mean texture 0
mean perimeter 0
mean area 0
mean smoothness 0
mean compactness 0
mean concavity 0
mean concave points 0
mean symmetry 0
mean fractal dimension 0
radius error 0
texture error 0
perimeter error 0
area error 0
smoothness error 0
compactness error 0
concavity error 0
concave points error 0
symmetry error 0
fractal dimension error 0
worst radius 0
worst texture 0
worst perimeter 0
worst area 0
worst smoothness 0
worst compactness 0
worst concavity 0
worst concave points 0
worst symmetry 0
worst fractal dimension 0
target 0
dtype: int64
Cantidad de muestras benignas(1) y malignas(0)⌗
df['target'].value_counts()
1 357
0 212
Name: target, dtype: int64
Grafica cantidad de muestras malignas y benignas⌗
sns.countplot(cancer['target'])
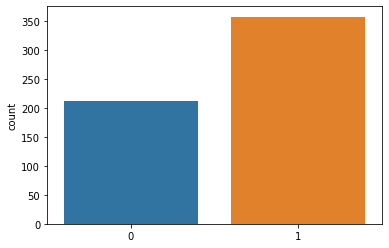
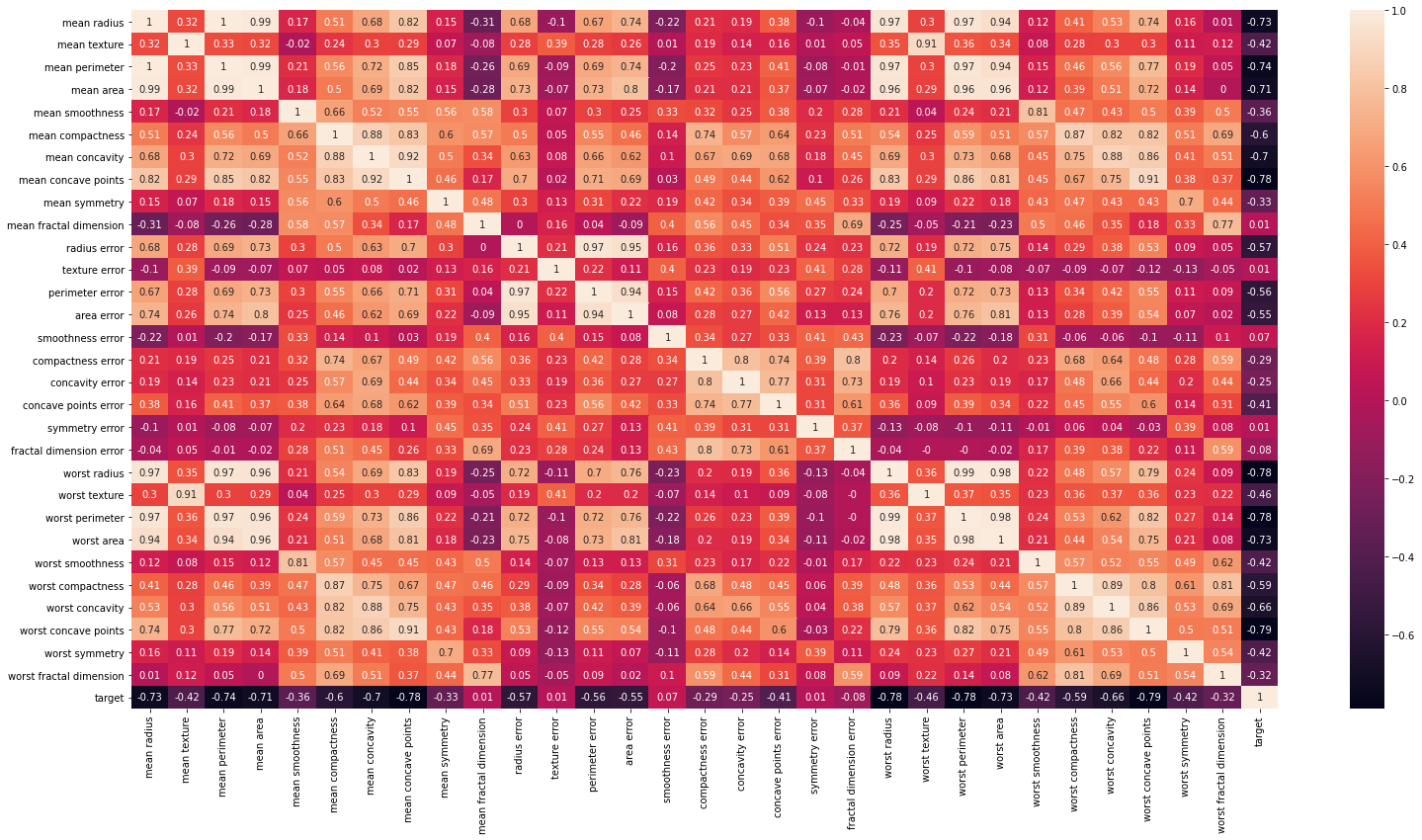
Creamos matriz de correlación⌗
plt.figure(figsize = (26,13))
correlation_matrix = df.corr().round(2)
sns.heatmap(data=correlation_matrix, annot=True)
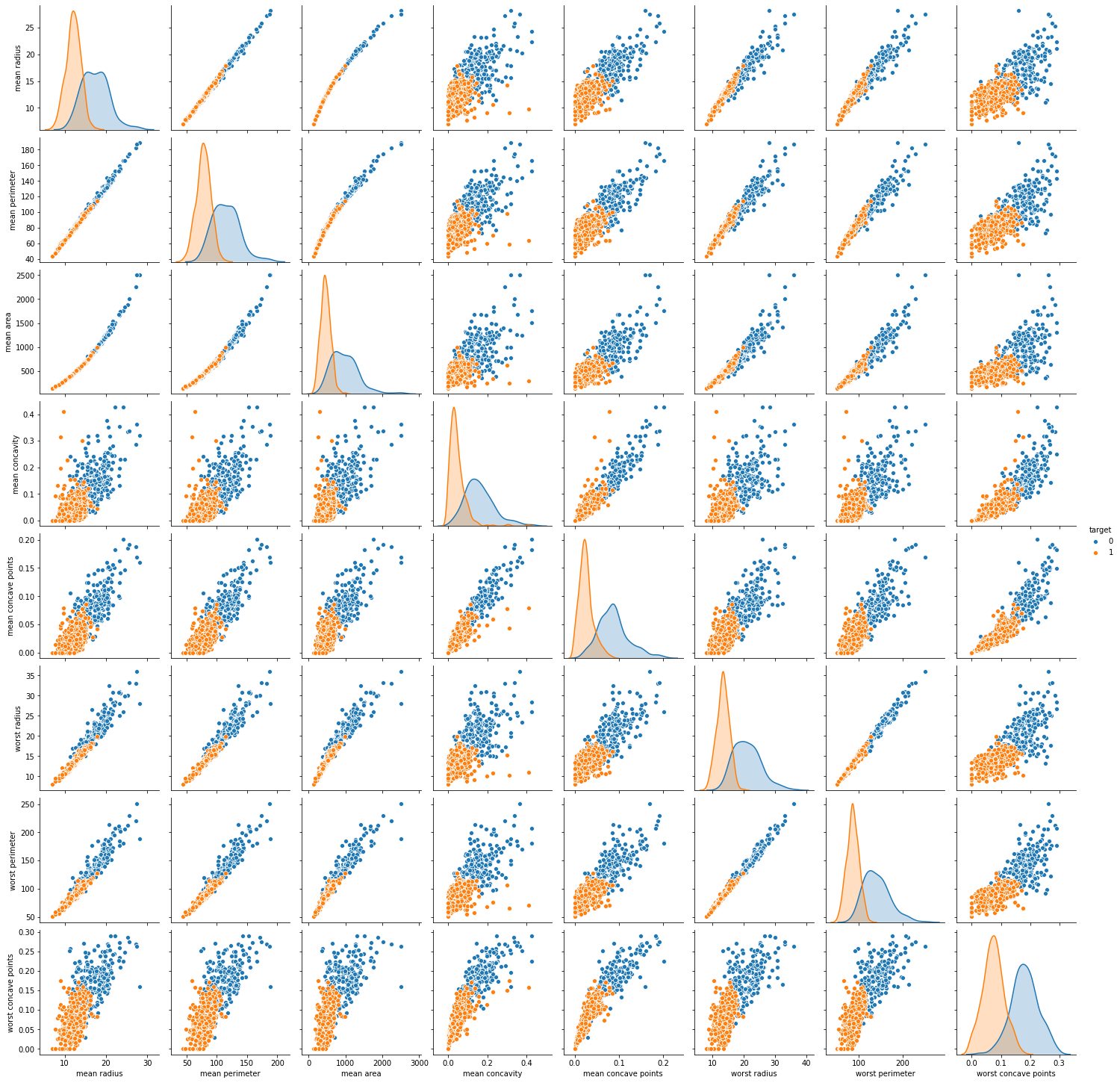
sns.pairplot(df, hue = 'target', vars = ['mean radius', 'mean perimeter', 'mean area',
'mean concavity', 'mean concave points', 'worst radius', 'worst perimeter', 'worst concave points'])
Creación y entrenamiento de modelo de tipo SVC (Support Vector Classification)⌗
x = df.drop(['target'], axis=1) # carga características a variable/dimensión/eje x
y = df['target'] # carga target a variable/dimensión/eje y
Dividimos el set de datos en subconjuntos de entrenamiento y test (75/25)⌗
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=0)
# crea modelo de tipo SVC, referencia: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
svc_model = SVC()
# entrena modelo con datos de entrenamiento
svc_model.fit(X_train, y_train)
# Obtiene resultados del modelo
svc_model.score(X_train, y_train)
0.903755868544601
y_train
293 1
332 1
565 0
278 1
489 0
..
277 0
9 0
359 1
192 1
559 1
Name: target, Length: 426, dtype: int64
predicciones = svc_model.predict(X_test)
print(classification_report(y_test, predicciones))
precision recall f1-score support
0 0.98 0.85 0.91 53
1 0.92 0.99 0.95 90
accuracy 0.94 143
macro avg 0.95 0.92 0.93 143
weighted avg 0.94 0.94 0.94 143
df2 = pd.DataFrame({'Real': y_test, 'Predecido': svc_model.predict(X_test).flatten()})
df2
| Real | Predecido | |
|---|---|---|
| 512 | 0 | 1 |
| 457 | 1 | 1 |
| 439 | 1 | 1 |
| 298 | 1 | 1 |
| 37 | 1 | 1 |
| … | … | … |
| 236 | 0 | 0 |
| 113 | 1 | 1 |
| 527 | 1 | 1 |
| 76 | 1 | 1 |
| 162 | 0 | 0 |
Ya con esto poseemos un algoritmo de tipo Support Vector Machine capaz de hacer tareas de clasificación en un set de datos específico. Se recomienda realizar cálculo de error del modelo y posibles optimizaciones a este.
